我院博士生研究生黄君烈和孟澄助理教授合作发表高水平论文

2025年5月，我院2022级博士生黄君烈（第一作者）、2021级博士生康欣来、2023级硕士生黄倩楠、2020级博士生李梦雨及孟澄助理教授（通讯作者）等合作的论文“Efficient Approximation of Leverage Scores in Two-dimensional Autoregressive Models with Application to Image Anomaly Detection”被国际统计学领域重要学术期刊《Journal of Computational and Graphical Statistics》接收。

论文概述

杠杆值用于量化数据集中各数据点的影响力，广泛应用于子抽样方法以提取具有代表性的子样本。本文针对二维自回归模型中杠杆值的计算与应用问题展开深入研究。基于其协变量矩阵的结构特性，我们创新性地提出了二维自回归模型杠杆值的递推计算公式，并据此设计了一种高效的近似计算算法。在理论层面，我们证明了该近似方法的误差上界，并对其计算复杂度进行了系统分析。通过广泛的数值模拟和真实数据实验，我们验证了该方法的性能、效率与稳健性，及其在超光谱图像异常检测任务中的价值。

二维自回归（Two-dimensional Autoregressive，简称2D AR）模型因其能刻画二维数据的特定结构而在图像处理、图像压缩任务中有很强的应用潜力。然而，用最小二乘方法拟合2D AR模型的计算复杂度较高，尤其在模型阶数未知的情况下，需要拟合不同阶数的模型以进行阶数选择，很大程度上限制了2D AR模型的实用价值。

本文提出了一种快速算法，可以高效地对2D AR模型进行模型阶数选择，杠杆值估计，和参数估计。对一个包含N个像素点，d个参数的2D AR模型，该算法可以将阶数选择中每个子模型的平均计算复杂度降至O(Nd)。算法得到参数估计的误差上界存在理论保证。大量数值实验表明，所提算法在保持与随机抽样相同时间复杂度的同时，实现了与杠杆值子抽样方法相当的参数估计精度。

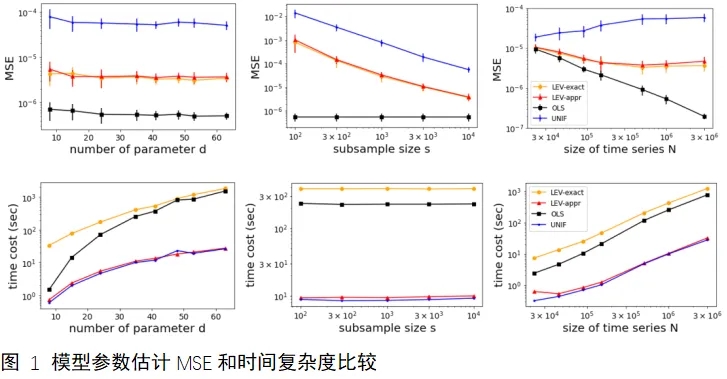
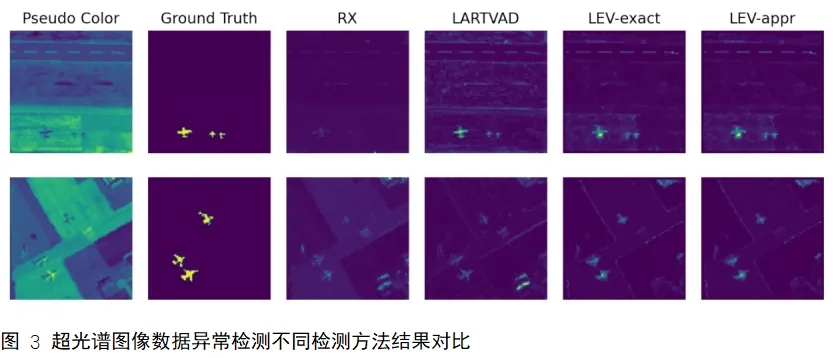
本文提出了一种基于2D AR模型杠杆值的图像异常检测方法。杠杆值量化了单个数据点在模型中的影响，而异常像素通常具有较高的杠杆值，因此2D AR模型的杠杆值可以自然地作为评估像素异常程度的一种指标。数值模拟实验结果显示，该方法在含有自相关噪声的低信噪比条件下仍能保持优异的异常检测性能，可准确识别图像中的异常像素区域。在真实数据上，相较于主流的图像异常检测方法，本方法不仅获得了更精确的检测结果，同时展现出显著的计算效率优势。

发表页面

作者简介

黄君烈，中国人民大学统计与大数据研究院2022级博士生，明理创新实验室Stat2Spark团队理事，主要研究方向为大数据子抽样、图像异常检测和非参数统计等。目前已有一篇论文被《Journal of Computational and Graphical Statistics》接收，曾入选全国工业统计学教学研究会青年统计学家协会年会博士生论坛获海报展示机会。深度参与华为“难题揭榜”，作为核心成员斩获一枚火花奖，两枚鼓励奖。

孟澄，统计与大数据研究院助理教授、博士生导师。中国大百科全书（第三卷）统计学卷-数据科学分卷副主编。主要研究方向为：大数据压缩、最优输运方法、统计及工业交叉科学等，在Biometrika, IEEE TPAMI, TNNLS, JMLR等期刊会议上发表论文二十余篇。主要研究方向为大数据快速算法、最优输运问题等，主持国自科青年基金。孟澄带领团队获得华为“难题揭榜”价值火花奖三枚、鼓励火花奖三枚，指导博士生李梦雨获得2024年度中国科协青年人才托举工程博士生专项计划（托举学会：中国现场统计研究会）。

实验室主页：https://cheng-bdal.github.io/Cheng-BDAL-CN.github.io/

学生发文一览

近年来，研究院博士生在国际顶级学术期刊上发表了9篇高水平学术论文。

1.Huijuan Zhou, Xianyang Zhang, Jun Chen (2020). Covariate Adaptive Family-wise Error Rate Control for Genome-Wide Association Studies. Biometrika. 108(4):915-931.

2.Hanzhong Liu, Fuyi Tu and Wei Ma (2023). Lasso-adjusted treatment effect estimation under covariate-adaptive randomization. Biometrika . 110(2): 431-447. 

3.Xing Yan, Yonghua Su, Wenxuan Ma（2023）. Adaptively flexible predictive distribution for uncertainty quantification. IEEE Transactions on Pattern Analysis and Machine Intelligence (TPAMI) . 45(11): 13068-13082. 

4.Wenxuan ma, Xing Yan and Kun Zhang (2023). Improving uncertainty quantification of variance networks by tree-structured learning. IEEE Transactions on Neural Networks and Learning Systems .

5.Yan, Y., & Luo, X. (2024). Bayesian integrative region segmentation in spatially resolved transcriptomic studies. Journal of the American Statistical Association . 119(547): 1709-1721.

6.Li, T., Meng, C., Xu, H., & Yu, J. (2024). Hilbert curve projection distance for distribution comparison. IEEE Transactions on Pattern Analysis and Machine Intelligence .46(7): 4993 - 5007. 

7.Yan Song, Wenlin Dai, Marc G. Genton (2024). Large-Scale Low-Rank Gaussian Process Prediction with Support Points. Journal of the American Statistical Association.

8.Ya Zhou, Raymond K W Wong, Kejun He (2024). Broadcasted nonparametric tensor regression. Journal of the Royal Statistical Society: Series B (Statistical Methodology).86(5): 1197 - 1220. 

9.Tao Li, Cheng Meng, Hongteng Xu and Jun Zhu (2025). Efficient Variants of Wasserstein Distance in Hyperbolic Space via Space-filling Curve Projection. IEEE Transactions on Neural Networks and Learning Systems , Just accepted.

2020年以来，研究院学生在统计学、计量经济、机器学习等领域国际一流学术期刊上发表了26篇高水平论文。

1.Tong Wang, Wei Ma (2021). The impact of misclassification on covariate‐adaptive randomized clinical trials. Biometrics .  77(2): 451-464.

2.Fei Ding, Shiyuan He, David Jones, Jianhua Z. Huang (2021). Functional PCA with covariate dependent mean and covariance structure. Technometrics . 64(3): 335-345.

3.Qiuyu Wu, Xiangyu Luo (2021). Nonparametric Bayesian Two-Level Clustering for Subject-Level Single-Cell Expression Data. Statistica Sinica .  32, 1835-1856.

4.Fangting Zhou, Kejun He, Qiwei Li, Robert S Chapkin, Yang Ni (2022). Bayesian biclustering for microbial metagenomic sequencing data via multinomial matrix factorization. Biostatistics .23(3): 891-909.

5.Chen Canyi,Zhu Liping(2022). Distributed Decoding From Heterogeneous 1-Bit Compressive Measurements. Journal of Computational and Graphical Statistics .  32(3): 884-894.

6.Zhang Yilin, Chen Canyi, andZhu Liping (2022). Sliced Independence Test. Statistica Sinica . 32, 2477­-2496. 

7.Chunrong Ai, Lukang Huang, Zheng Zhang (2022). A simple and efficient estimation of average treatment effects in models with unmeasured confounders. Statistica Sinica .  32, 1007-1026.

8.Mengyu Li, Junlong Zhao (2022). Communication-Efficient Distributed Linear Discriminant Analysis for Binary Classification. Statistica Sinica . 32, 1343-1361.

9.Qiuyu Wu, Xiangyu Luo (2022). Estimating heterogeneous gene regulatory networks from zero-inflated single-cell expression data. Annals of Applied Statistics .  16(4): 2183-2200.

10.Yinqiao Yan, Xiangyu Luo (2023). Bayesian Tree-Structured Two-Level Clustering for Nested Data Analysis. Journal of Computational and Graphical Statistics .  32(3): 1185-1194.

11.Mengyu Li, Jun Yu, Hongteng Xu, and Cheng Meng (2023). Efficient Approximation of Gromov-Wasserstein Distance Using Importance Sparsification. Journal of Computational and Graphical Statistics , 32:4, 1512-1523

12.Chen Canyi, Gu Yuwen, Zou Hui, and Zhu Liping (2023). Distributed Sparse Composite Quantile Regression in Ultrahigh Dimensions. Statistica Sinica .  33, 1143-1167. 

13.Cao Jiahao, He Shiyuan, and Zhang Bohai (2023). Spatial Linear Regression with Covariate Measurement Errors: Inference and Scalable Computation in a Functional Modeling Approach. Journal of Computational and Graphical Statistics , 32:4, 1588-1599. 

14.Dai Wenlin,Song Yan, Wang Dianpeng (2023). A subsampling method for regression problems based on minimum energy criterion.Technometrics .  65(2): 192-205.

15.Mengyu Li, Jun Yu, Tao Li, Cheng Meng (2023). Importance Sparsification for Sinkhorn Algorithm. Journal of Machine Learning Research . 24(247): 1−44.

16.Shuoli Chen, Kejun He, Shiyuan He, Yang Ni, Raymond K. W. Wong (2023). Bayesian Nonlinear Tensor Regression with Functional Fused Elastic Net Prior. Technometric s . 65(4), 524-536.

17.Zhang Fengyu, Zhou Ya, He Kejun, Wong Raymond (2023). Multivariate Varying-coefficient Models via Tensor Decomposition. Statistica Sinica . 34:4, 2015-2042

18.Gu, Y., Liu, H., and Ma, W. (2023). Regression-based multiple treatment effect estimation under covariate-adaptive randomization. Biometrics , 79(4), 2869–2880.

19.Li, T., Yu, J., & Meng, C. (2023). Scalable model-free feature screening via sliced-wasserstein dependency. Journal of Computational and Graphical Statistics , 32(4), 1501-1511.

20.Zhang, Y., & Yang, S. (2024). Kernel Angle Dependence Measures in Metric Spaces. Journal of Computational and Graphical Statistics , (just-accepted), 1-19.

21.Mengyu Li, Jingyi Zhang & Cheng Meng (2024). Nonparametric additive models for billion observations. Journal of Computational and Graphical Statistics . 33(4),1397-1412.

22.Haosheng Shi and Wenlin Dai (2024). A community Hawkes model for continuous-time networks with interaction heterogeneity. Accepted by Statistica Sinica .

23.Delin Zhao and Liping Zhu(2024). Detect Complete Dependence via Trace Correlation in the Presence of Matrix-Valued Random Objects. Statistica Sinica .

24.Ziya Xu and Sai Li (2024). Leveraging Local Distributions in Mendelian Randomization: Uncertain Opinions are Invalid. Statistica Sinica .

25.Wu Z, Jiang W, Xu X. (2024). Applicationsoffunctionaldependencetospatialeconometrics. Econometric Theory . Published online 2024:1-36.

26.Huang, J., Kang, X., Huang, Q., Li, M., Meng, C., & Zhang, J. (2025). Efficient Approximation of Leverage Scores in Two-dimensional Autoregressive Models with Application to Image Anomaly Detection. Journal of Computational and Graphical Statistics, 1–19.